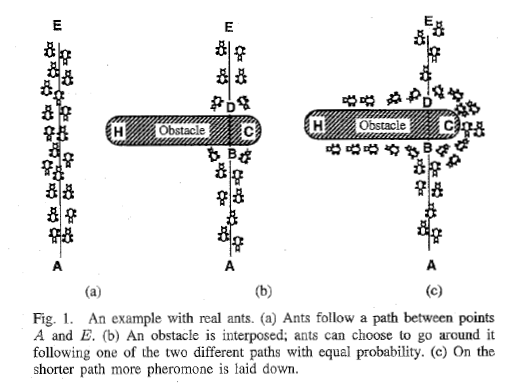
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
|
import random
import copy
import time
import sys
import math
import tkinter
import threading
from functools import reduce
'''
ALPHA:信息启发因子,值越大,则蚂蚁选择之前走过的路径可能性就越大
,值越小,则蚁群搜索范围就会减少,容易陷入局部最优
BETA:Beta值越大,蚁群越就容易选择局部较短路径,这时算法收敛速度会
加快,但是随机性不高,容易得到局部的相对最优
'''
(ALPHA, BETA, RHO, Q) = (1.0,2.0,0.5,100.0)
(city_num, ant_num) = (50,50)
distance_x = [
178,272,176,171,650,499,267,703,408,437,491,74,532,
416,626,42,271,359,163,508,229,576,147,560,35,714,
757,517,64,314,675,690,391,628,87,240,705,699,258,
428,614,36,360,482,666,597,209,201,492,294]
distance_y = [
170,395,198,151,242,556,57,401,305,421,267,105,525,
381,244,330,395,169,141,380,153,442,528,329,232,48,
498,265,343,120,165,50,433,63,491,275,348,222,288,
490,213,524,244,114,104,552,70,425,227,331]
distance_graph = [ [0.0 for col in range(city_num)] for raw in range(city_num)]
pheromone_graph = [ [1.0 for col in range(city_num)] for raw in range(city_num)]
class Ant(object):
def __init__(self,ID):
self.ID = ID
self.__clean_data()
def __clean_data(self):
self.path = []
self.total_distance = 0.0
self.move_count = 0
self.current_city = -1
self.open_table_city = [True for i in range(city_num)]
city_index = random.randint(0,city_num-1)
self.current_city = city_index
self.path.append(city_index)
self.open_table_city[city_index] = False
self.move_count = 1
def __choice_next_city(self):
next_city = -1
select_citys_prob = [0.0 for i in range(city_num)]
total_prob = 0.0
for i in range(city_num):
if self.open_table_city[i]:
try :
select_citys_prob[i] = pow(pheromone_graph[self.current_city][i], ALPHA) * pow((1.0/distance_graph[self.current_city][i]), BETA)
total_prob += select_citys_prob[i]
except ZeroDivisionError as e:
print ('Ant ID: {ID}, current city: {current}, target city: {target}'.format(ID = self.ID, current = self.current_city, target = i))
sys.exit(1)
if total_prob > 0.0:
temp_prob = random.uniform(0.0, total_prob)
for i in range(city_num):
if self.open_table_city[i]:
temp_prob -= select_citys_prob[i]
if temp_prob < 0.0:
next_city = i
break
if (next_city == -1):
next_city = random.randint(0, city_num - 1)
while ((self.open_table_city[next_city]) == False):
next_city = random.randint(0, city_num - 1)
return next_city
def __cal_total_distance(self):
temp_distance = 0.0
for i in range(1, city_num):
start, end = self.path[i], self.path[i-1]
temp_distance += distance_graph[start][end]
end = self.path[0]
temp_distance += distance_graph[start][end]
self.total_distance = temp_distance
def __move(self, next_city):
self.path.append(next_city)
self.open_table_city[next_city] = False
self.total_distance += distance_graph[self.current_city][next_city]
self.current_city = next_city
self.move_count += 1
def search_path(self):
self.__clean_data()
while self.move_count < city_num:
next_city = self.__choice_next_city()
self.__move(next_city)
self.__cal_total_distance()
class TSP(object):
def __init__(self, root, width = 800, height = 600, n = city_num):
self.root = root
self.width = width
self.height = height
self.n = n
self.canvas = tkinter.Canvas(
root,
width = self.width,
height = self.height,
bg = "#EBEBEB",
xscrollincrement = 1,
yscrollincrement = 1
)
self.canvas.pack(expand = tkinter.YES, fill = tkinter.BOTH)
self.title("TSP蚁群算法(n:初始化 e:开始搜索 s:停止搜索 q:退出程序)")
self.__r = 5
self.__lock = threading.RLock()
self.__bindEvents()
self.new()
for i in range(city_num):
for j in range(city_num):
temp_distance = pow((distance_x[i] - distance_x[j]), 2) + pow((distance_y[i] - distance_y[j]), 2)
temp_distance = pow(temp_distance, 0.5)
distance_graph[i][j] =float(int(temp_distance + 0.5))
def __bindEvents(self):
self.root.bind("q", self.quite)
self.root.bind("n", self.new)
self.root.bind("e", self.search_path)
self.root.bind("s", self.stop)
def title(self, s):
self.root.title(s)
def new(self, evt = None):
self.__lock.acquire()
self.__running = False
self.__lock.release()
self.clear()
self.nodes = []
self.nodes2 = []
for i in range(len(distance_x)):
x = distance_x[i]
y = distance_y[i]
self.nodes.append((x, y))
node = self.canvas.create_oval(x - self.__r,
y - self.__r, x + self.__r, y + self.__r,
fill = "#ff0000",
outline = "#000000",
tags = "node",
)
self.nodes2.append(node)
self.canvas.create_text(x,y-10,
text = '('+str(x)+','+str(y)+')',
fill = 'black'
)
for i in range(city_num):
for j in range(city_num):
pheromone_graph[i][j] = 1.0
self.ants = [Ant(ID) for ID in range(ant_num)]
self.best_ant = Ant(-1)
self.best_ant.total_distance = 1 << 31
self.iter = 1
def line(self, order):
self.canvas.delete("line")
def line2(i1, i2):
p1, p2 = self.nodes[i1], self.nodes[i2]
self.canvas.create_line(p1, p2, fill = "#000000", tags = "line")
return i2
reduce(line2, order, order[-1])
def clear(self):
for item in self.canvas.find_all():
self.canvas.delete(item)
def quite(self, evt):
self.__lock.acquire()
self.__running = False
self.__lock.release()
self.root.destroy()
print (u"\n程序已退出...")
sys.exit()
def stop(self, evt):
self.__lock.acquire()
self.__running = False
self.__lock.release()
def search_path(self, evt = None):
self.__lock.acquire()
self.__running = True
self.__lock.release()
while self.__running:
for ant in self.ants:
ant.search_path()
if ant.total_distance < self.best_ant.total_distance:
self.best_ant = copy.deepcopy(ant)
self.__update_pheromone_gragh()
print (u"迭代次数:",self.iter,u"最佳路径总距离:",int(self.best_ant.total_distance))
self.line(self.best_ant.path)
self.title("TSP蚁群算法(n:随机初始 e:开始搜索 s:停止搜索 q:退出程序) 迭代次数: %d" % self.iter)
self.canvas.update()
self.iter += 1
def __update_pheromone_gragh(self):
temp_pheromone = [[0.0 for col in range(city_num)] for raw in range(city_num)]
for ant in self.ants:
for i in range(1,city_num):
start, end = ant.path[i-1], ant.path[i]
temp_pheromone[start][end] += Q / ant.total_distance
temp_pheromone[end][start] = temp_pheromone[start][end]
for i in range(city_num):
for j in range(city_num):
pheromone_graph[i][j] = pheromone_graph[i][j] * RHO + temp_pheromone[i][j]
def mainloop(self):
self.root.mainloop()
if __name__ == '__main__':
TSP(tkinter.Tk()).mainloop()
|