模拟退火算法

模拟退火算法（SA）

1.简介

​ 模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。根据 Metropolis 准则，粒子在温度T时趋于平衡的概率为 e-ΔE/(kT) ，其中 E 为温度 T 时的内能， ΔE 为其改变量， k 为 Boltzmann 常数。用固体退火模拟组合优化问题，将内能E模拟为目标函数值 f ，温度 T 演化成控制参数 t ，即得到解组合优化问题的模拟退火算法：由初始解 i 和控制参数初值 t 开始，对当前解重复“产生新解计算目标函数差接受或舍弃”的迭代，并逐步衰减t值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表 (Cooling Schedule) 控制，包括控制参数的初值 t 及其衰减因子 Δt 、每个 t 值时的迭代次数 L 和停止条件 S 。

2.模型

模拟退火算法可以分解为解空间、目标函数和初始解三部分。

3.基本思想

(1) 初始化：初始温度 T (充分大)，初始解状态 S (是算法迭代的起点)， 每个 T 值的迭代次数 L

(2) 对 k=1，……，L 做第 3 至第 6 步：

(3) 产生新解 S'

(4) 计算增量 Δt′=C(S′)-C(S) ，其中 C(S) 为评价函数

(5) 若 Δt′<0 则接受 S′ 作为新的当前解，否则以概率 exp(-Δt′/T) 接受 S′ 作为新的当前解.

(6) 如果满足终止条件则输出当前解作为最优解，结束程序。 终止条件通常取为连续若干个新解都没有被接受时终止算法。

(7) T 逐渐减少，且 T->0 ，然后转第 2 步。

模拟退火的算法流程图如下:

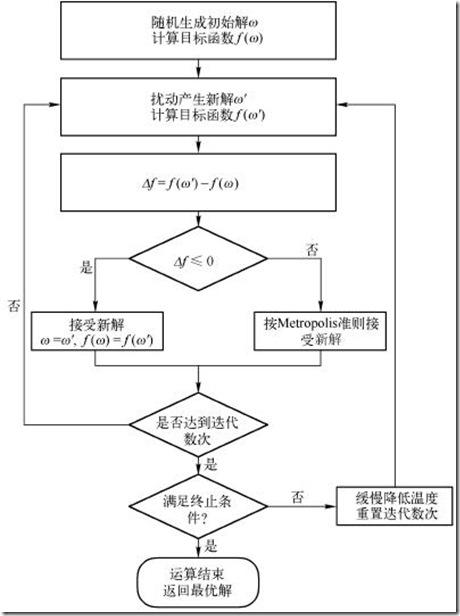
模拟退火算法新解的产生和接受可分为如下四个步骤：

第一步是由一个产生函数从当前解产生一个位于解空间的新解；为便于后续的计算和接受，减少算法耗时，通常选择由当前新解经过简单地变换即可产生新解的方法，如对构成新解的全部或部分元素进行置换、互换等，注意到产生新解的变换方法决定了当前新解的邻域结构，因而对冷却进度表的选取有一定的影响。

第二步是计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生，所以目标函数差的计算最好按增量计算。事实表明，对大多数应用而言，这是计算目标函数差的最快方法。

第三步是判断新解是否被接受,判断的依据是一个接受准则，最常用的接受准则是 Metropolis 准则: 若 Δt′<0 则接受 S′ 作为新的当前解 S ，否则以概率 exp(-Δt′/T) 接受 S′ 作为新的当前解 S 。

第四步是当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可。此时，当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时，则在原当前解的基础上继续下一轮试验。模拟退火算法与初始值无关，算法求得的解与初始解状态 S (是算法迭代的起点)无关；模拟退火算法具有渐近收敛性，已在理论上被证明是一种以概率 l 收敛于全局最优解的全局优化算法；模拟退火算法具有并行性

想象一下如果我们现在有下面这样一个函数，现在想求函数的（全局）最优解。如果采用 Greedy 策略，那么从 A 点开始试探，如果函数值继续减少，那么试探过程就会继续。而当到达点B时，显然我们的探求过程就结束了（因为无论朝哪个方向努力，结果只会越来越大）。最终我们只能找打一个局部最后解 B 。

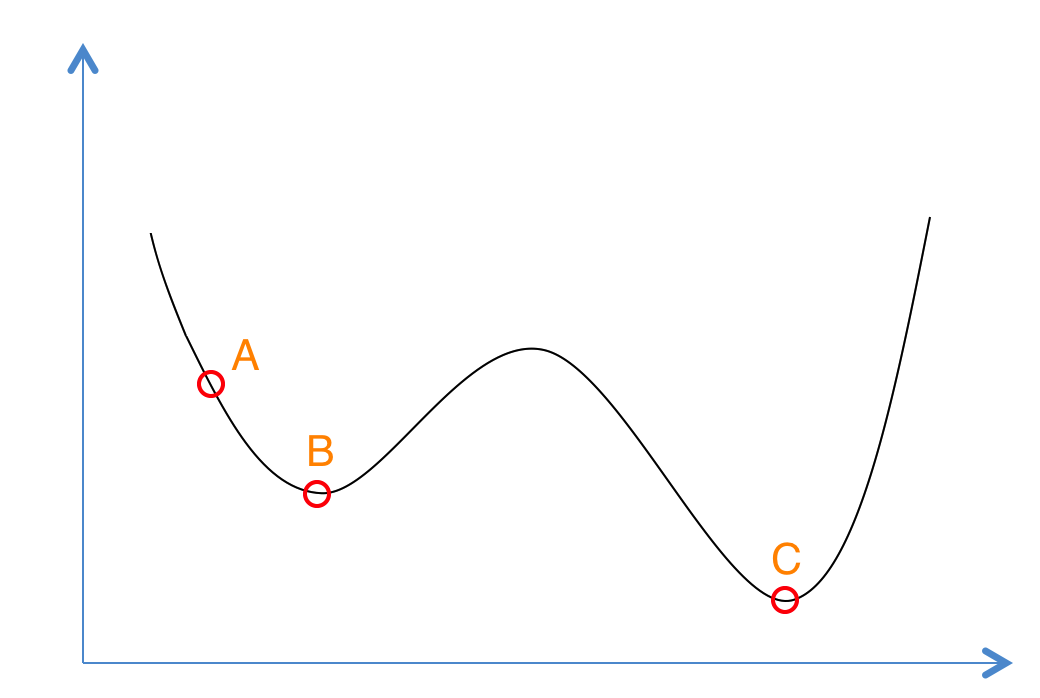
模拟退火其实也是一种 Greedy 算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以上图为例，模拟退火算法在搜索到局部最优解 B 后，会以一定的概率接受向右继续移动。也许经过几次这样的不是局部最优的移动后会到达 B 和 C 之间的峰点，于是就跳出了局部最小值B。

根据Metropolis准则，粒子在温度T时趋于平衡的概率为 exp(-ΔE/(kT)) ，其中 E 为温度 T 时的内能，ΔE为其改变数, k 为 Boltzmann 常数。 Metropolis 准则常表示为

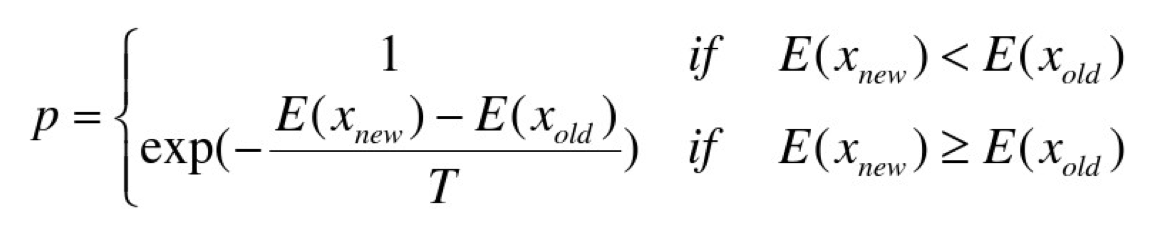
Metropolis 准则表明，在温度为 T 时，出现能量差为 dE 的降温的概率为 P(dE)，表示为： P(dE) = exp(dE/(kT)) 。其中 k 是一个常数， exp 表示自然指数，且 dE<0 。所以 P 和 T 正相关。这条公式就表示：温度越高，出现一次能量差为 dE 的降温的概率就越大；温度越低，则出现降温的概率就越小。又由于 dE 总是小于 0 （因为退火的过程是温度逐渐下降的过程），因此 dE/kT < 0 ，所以 P(dE) 的函数取值范围是 (0,1) 。随着温度 T 的降低， P(dE) 会逐渐降低。
我们将一次向较差解的移动看做一次温度跳变过程，我们以概率 P(dE) 来接受这样的移动。也就是说，在用固体退火模拟组合优化问题，将内能E模拟为目标函数值 f，温度T演化成控制参数 t，即得到解组合优化问题的模拟退火演算法：由初始解 i 和控制参数初值 t 开始，对当前解重复“产生新解计算目标函数差接受或丢弃”的迭代，并逐步衰减 t 值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表 (Cooling Schedule) 控制，包括控制参数的初值 t 及其衰减因子 Δt 、每个 t 值时的迭代次数 L 和停止条件 S 。

总结起来就是：

• 若 f( Y(i+1) ) <= f( Y(i) ) (即移动后得到更优解)，则总是接受该移动；
• 若 f( Y(i+1) ) > f( Y(i) ) (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）相当于上图中，从 B 移向 BC 之间的小波峰时，每次右移（即接受一个更糟糕值）的概率在逐渐降低。如果这个坡特别长，那么很有可能最终我们并不会翻过这个坡。如果它不太长，这很有可能会翻过它，这取决于衰减 t 值的设定。

关于普通 Greedy 算法与模拟退火，有一个有趣的比喻：

• • 普通 Greedy 算法：兔子朝着比现在低的地方跳去。它找到了不远处的最低的山谷。但是这座山谷不一定最低的。这就是普通 Greedy 算法，它不能保证局部最优值就是全局最优值。
  • 模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向低处，也可能踏入平地。但是，它渐渐清醒了并朝最低的方向跳去。这就是模拟退火。

4.TSP问题的matlab求解

1. TSP问题：TSP(Traveling salesman problem)即旅行商问题，旅行商希望在N个城市进行一次巡回旅行，可以恰好访问每一个城市一次，并且最终回到出发城市。并且要使得这次巡回旅行的总消耗最小（总距离或总花销等等），如何求这个路线？

• TSP的解空间S是遍历每个城市恰好一次的所有回路（回到起点），那么一个可行解即为所有城市的一个排列，则解空间可以表示为：

即为每个城市的编号，其中的每一个排列 即为一个离线，所以初始解就被表示成为了一个{1,2,…,N}的随机序列。

2. 目标函数

遍历所有城市的代价最小，此处我们将代价刻画为总路径最小，目标函数：

而 即为该最短路径（TSP问题的解即为城市标号的一个排列）

3. 新解的产生

• 两点交换法：交换 的访问顺序
• 三变换：任选序号 ,将 之间的路径插到 之后访问。

4. Metropolis接收准则

以新解与当前解的目标函数差（内能之差）来定义接受概率：

TSP问题的matlab程序

function  SA_TSP()
% Input: The coordinates of different cities
data=[565,575;25,185;345,750;945,685;845,355;880,460;25,230;525,1000;580,1175;650,1130;1605,620;1220,580;1465,200;1530,5;845,680;725,370];
num_city = size(data,1);
Initial_temp = 1000;
res = 1e-3;                             % 最低温限制
ratio = 0.9;                            % 降温参数，控制温度的下降
temperature = Initial_temp;
Markov_length = 1000;                   % 改变解的次数
Distance_matrix = pdist2(data,data);    % 矩阵的形式存储城市之间的距离
route_new = randperm(num_city);         % 新产生的解路线
Energy_current = inf;                   % 当前解的能量
Energy_best = inf;                      % 最优解的能量

route_current = route_new;              % 当前解路线
route_best = route_new;                 % 最优解路线
pic_num = 1;

% 外层while循环控制降温过程，内层for循环控制新解的产生。
while temperature > res
    Energy1=Energy_best;                             % 用于控制循环的结束条件
    for i = 1: Markov_length
        
        % 产生新解(对当前解添加扰动)
        if rand >0.5
            % 两点交换
            a = 0;
            b = 0;
            while (a==b)
                a = ceil(rand*num_city);
                b = ceil(rand*num_city);
            end
            temp = route_new(a);
            route_new(a) = route_new(b);
            route_new(b) = temp;
        else
            % 三变化
            factor = randperm(num_city,3);
            factor = sort(factor);      % 对三个元素排序，a<b<c
            a = factor(1);
            b = factor(2);
            c = factor(3);
            temp = route_new(a:b);
            route_new(a:a+c-b-1) = route_new(b+1:c);
            route_new(a+c-b:c) = temp;
        end
        
        Energy_new = 0;   %计算该条路线的总距离
        for j=1:num_city-1
            Energy_new = Energy_new + Distance_matrix(route_new(j),route_new(j+1));
        end
        % 回到起始点，加上首尾两个城市的距离
        Energy_new = Energy_new+Distance_matrix(route_new(1),route_new(num_city));
        
        
        % 按照Metroplis准则接收新解
        if Energy_new<Energy_current
            % 更新局部最优
            Energy_current = Energy_new;
            route_current = route_new;
            
            % 更新全局最优
            if Energy_new<Energy_best
                Energy_best=Energy_new;
                route_best = route_new;
            end
            
        else
            if rand<exp(-(Energy_new-Energy_current)/temperature)
                Energy_current = Energy_new;
                route_current = route_new;
            else
                route_new = route_current; % 否则路线不更新，保存更改之前的路线
            end
            
        end
        
    end
    
    %plots
    items = [route_new,route_new(1)];                % 从最后一个城市回到起始城市

    scatter(data(route_new,1),data(route_new,2))
    for i=1:length(route_new)
        text(data(route_new(i),1),data(route_new(i),2),num2str(items(i)))
    end
    
    hold on
    plot(data(items,1),data(items,2),'b-')
    text(1200,1000,['Temp=',num2str(temperature)]);
    text(1200,950,['Distance=',num2str(Energy_best)]);
    drawnow;
    F=getframe(gcf);
    I=frame2im(F);
    [I,map]=rgb2ind(I,256);
    if pic_num == 1
        imwrite(I,map,'TSP.gif','gif', 'Loopcount',inf,'DelayTime',2);
    else
        imwrite(I,map,'TSP.gif','gif','WriteMode','append','DelayTime',2);
    end
    hold off
    title('SA Algorithm for TSP problem')
    xlabel('X coordinate')
    ylabel('Y coordinate')
    pic_num = pic_num + 1;

    if Energy1==Energy_best&&Energy_current==Energy_best
        break
    else
        temperature = temperature*ratio; %降温过程
    end
    
end

%Energy_best:最短路径；route_best:最短路径对应的最优距离（不唯一）
disp('The best route is:');disp([route_best,route_best(1)])
disp(['The smallest distance:',num2str(round(Energy_best,8))]);

其中一次运行结果：

The best route is:

16 5 6 14 13 11 12 4 15 10 9 8 3 7 2 1 16

The smallest distance:5101.7451

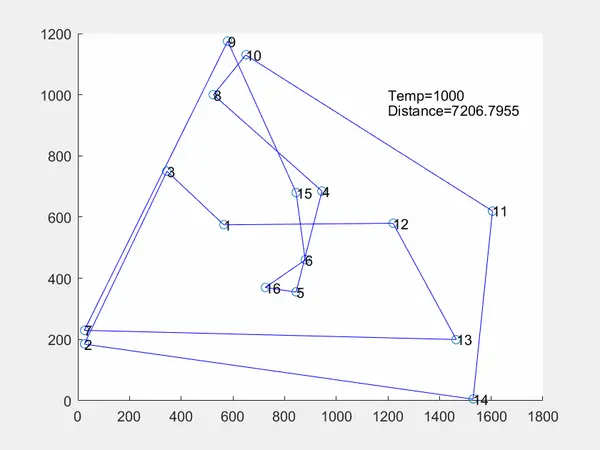
​ 模拟退火算法搜索过程