粒子群算法
粒子群算法(PSO)
1.简介
1995年,美国学者Kennedy和Eberhart共同提出了粒子群算法,其基本思想源于对鸟类群体行为进行建模与仿真的研究结果的启发。
粒子群优化算法(PSO:Particle swarm optimization) 是一种进化计算技术,源于对鸟群捕食的行为研究。它的核心思想是利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的可行解。
PSO的优势在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。
现在我们赋予鸟儿一些参数:
:个体学习因子,也称为个体加速因子。这个因子越大,鸟儿越倾向于飞往它自己曾去的食物量最多的地方
:社会学系因子,也成为社会加速因子。这个因子越大,鸟儿越倾向于飞往其他鸟儿(同伴们)曾去的食物量最多的地方
:[0,1]上的随机数。随机代表着鸟儿比较佛系,他也不知道飞哪里
:惯性权重,也叫惯性系数,这个数越大,代表着它不容易更改之前的运动路线,更倾向于探索未知领域。
因此图像变成了这样:
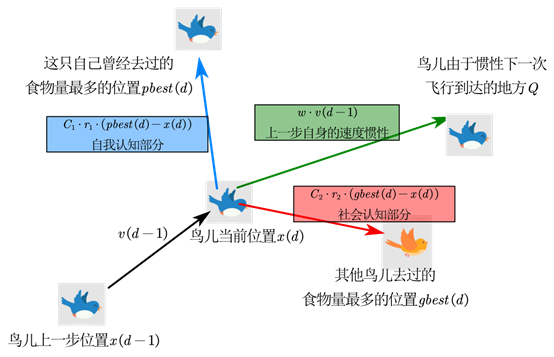
因此这只鸟第![[公式]](/img/loading.gif)
![[公式]](/img/loading.gif)
![[公式]](/img/loading.gif)
这只鸟第![[公式]](/img/loading.gif)
每运动一次,位置P和Q都会不断发生变化,最后会收敛到一个位置,这个位置就是食物最多的一个位置,如下动图所示:
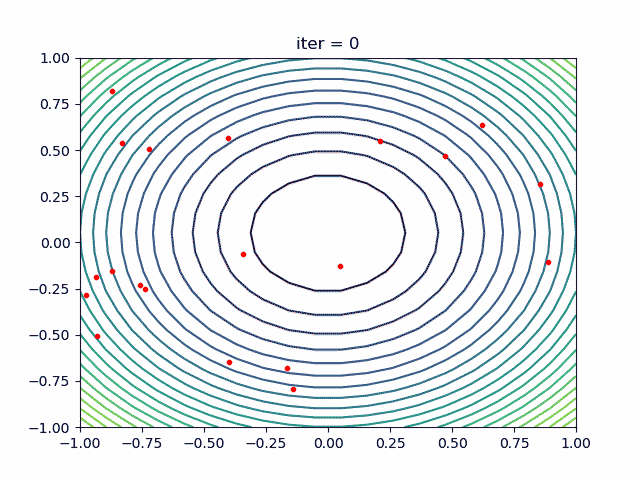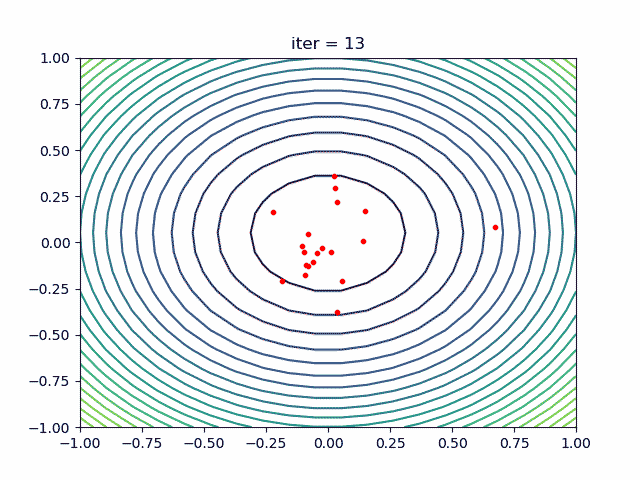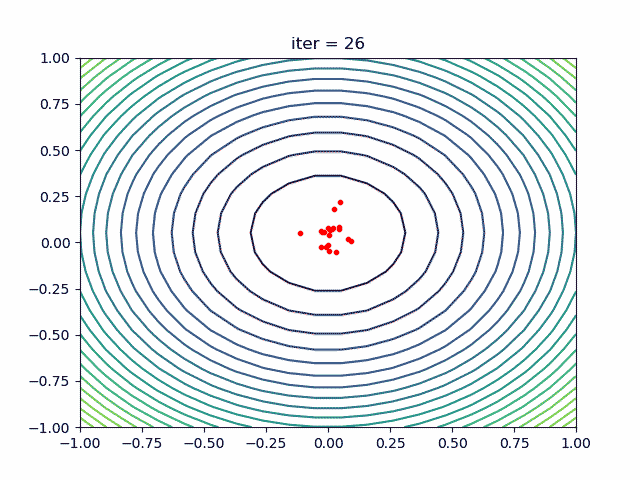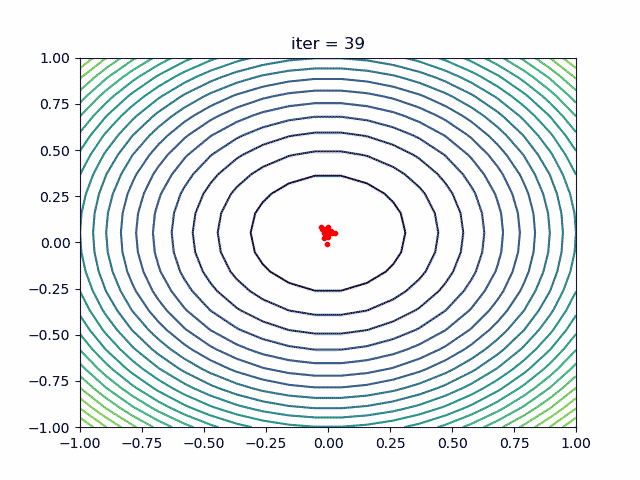
2.基本概念
每只鸟在某处位置能够找到食物的可能可以通过适应值来刻画,每只鸟能够记住自己的觅食位置,并且找到其中的最佳位置(局部最优,相当于极值点),鸟群中所有个体的最佳位置就可以看做整个鸟群的最佳觅食点(全局最优,相当于最值点)。可以预见的是,整个鸟群的觅食活动总体上一定是往这个全局最优的觅食区域运动的,通过鸟群觅食位置的不断移动即不断地迭代,速度的不断更新,鸟群往该最优位置步步逼近。
- 粒子:优化问题的候选解
- 位置:候选解所在的位置
- 速度:候选解移动的速度
- 适应度:评价粒子优劣的值,一般设置为目标函数值
- 个体最佳位置:单个粒子迄今为止找到的最佳位置
- 群体最佳位置:所有粒子迄今为止找到的最佳位置
3.算法流程
流程图如下:
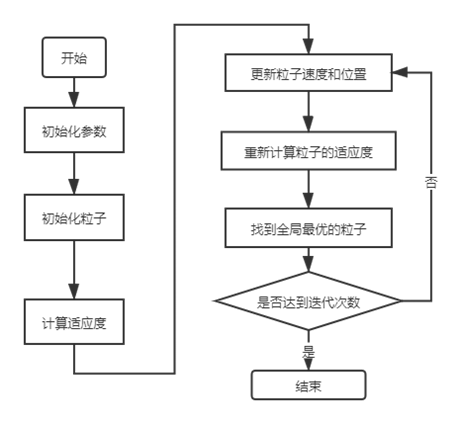
1.初始化粒子群。包括粒子的初始位置及速度,惯性因子等参数值
粒子数M一般选取20~40个,不过对于一些特殊的难题需要更多的粒子,粒子数量越多,搜索范围就越广,越容易找到全局最优解,但是也会带来更大的计算消耗。
评价各个粒子的初始适应值。
将初始的适应值作为各个粒子的局部最优解,保存各粒子的最优位置。并找到其中的最优值,作为全局最优解的初值,并记录其位置
更新粒子速度及位置
计算更新后粒子的适应值,更新每个粒子的局部最优值以及整个粒子群的全局最优值。
重复4~5直至满足迭代结束条件
粒子群算法中的符号说明:
:粒子个数
:粒子的个体学习因子,也称为个体加速因子
:粒子的社会学习因子,也称为社会加速因子
:速度的惯性权重
:第d次迭代时,第i个粒子的速度
:第d次迭代时,第i个粒子所在的位置
:在位置x时的适应度值(一般取目标函数值)
:到第d次迭代为止,第i个粒子经过的最好的位置
:到第d次迭代为止,所有粒子经过的最好的位置
4.核心公式:
粒子群算法最主要是掌握以下公式: 这只鸟第![[公式]](/img/loading.gif)
这只鸟第![[公式]](/img/loading.gif)
![[公式]](/img/loading.gif)
![[公式]](/img/loading.gif)
5.重要参数
5.1学习因子
在最初提出粒子群算法的论文中指出,个体学习因子和社会学习因子取2比较合适。
学习因子也是非负常数,是调整局部最优值和全局最优值权重的参数,如果前者为0说明搜寻过程中没有自身经验只有社会经验,容易陷入局部最优解;若后者为0,即只有社会经验,没有自身经验,常常会陷入局部最优解中,不能飞越该局部最优区域。
5.2惯性权重
对算法的收敛起到很大的作用,其值越大,粒子飞跃的范围就越广,更容易找到全局最优,但是也会错失局部搜寻的能力。
一般来说惯性权重取0.9‐1.2是比较合适的,一般取0.9就行。
5.3种群数量
粒子群算法的最大特点就是速度快,因此初始种群取50-1000都是可以的,虽然初始种群越大收敛性会更好,不过太大了也会影响速度;
5.4 迭代次数
一般取100~4000,太少解不稳定,太多浪费时间。对于复杂问题,进化代数可以相应地提高;
5.5 空间维数
粒子搜索的空间维数即为自变量的个数。比如求一元函数的最值就是一维空间,n元函数的最值就是n维空间
5.6 位置限制
限制粒子搜索的空间,即自变量的取值范围,对于无约束问题此处可以省略。
5.7 速度限制
如果粒子飞行速度过快,很可能直接飞过最优解位置,但是如果飞行速度过慢,会使得收敛速度变慢,因此设置合理的速度限制就很有必要了。
6.代码实现
6.1基于numpy
1 | |
6.2 基于sko.pso
python sko库中包含了常用的启发式算法, 也包含粒子群算法PSO,可以直接调用,非常快捷方便 。
1 | |